LABORATORIO NRO. 2

DISEÑO DE CIRCUITOS COMBINACIONALES

COMPETENCIA ESPECIFICA DE LA SESIÓN: 

• Comprobar las tablas de verdad de puertas lógicas y sus combinaciones. 
• Conocer las principales Puertas Lógicas, su simbología y comportamiento 
• Utilizar un SIMULADOR para comprobar el comportamiento de los mismos. 
• Utilizar métodos de simplificación de compuertas lógicas. 

 MARCO TEÓRICO:

INPUT		OUTPUT
A	B	A NAND B
0	0	1
0	1	1
1	0	1
1	1	0

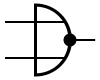
La puerta NAND, compuerta NAND o NOT AND :

Es una puerta lógica que produce una salida falsa solamente si todas sus entradas son verdaderas; por tanto, su salida es complemento a la de la puerta AND, -se comporta de acuerdo a la tabla de verdad mostrada a la derecha. Cuando todas sus entradas están en 1 (uno) o en ALTA, su salida está en 0 o en BAJA, mientras que cuando una sola de sus entradas o ambas están en 0 o en BAJA, su SALIDA va a estar en 1 o en ALTA.

Se puede ver claramente que la salida X solamente es "0" (0 lógico, nivel bajo) cuando la entrada A como la entrada B están en "1". En otras palabras la salida X es igual a 0 cuando la entrada A y la entrada B son 1.

La puerta NAND es significativa debido a que cualquier función booleana se puede implementar mediante el uso de una combinación de puertas NAND. Esta propiedad se llama integridad funcional.

Los sistemas digitales que emplean ciertos circuitos lógicos se aprovechan de integridad funcional de NAND.

Simbolo:

Símbolo ANSI o "Militar"	Símbolo IEC	Símbolo DIN

INPUT		OUTPUT
A	B	A NOR B
0	0	1
0	1	0
1	0	0
1	1	0

La puerta NOR o compuerta NOR:

Es una puerta lógica digital que implementa la disyunción lógica negada -se comporta de acuerdo a la tabla de verdad mostrada a la derecha. Cuando todas sus entradas están en 0 (cero) o en BAJA, su salida está en 1 o en ALTA, mientras que cuando una sola de sus entradas o ambas están en 1 o en ALTA, su SALIDA va a estar en 0 o en BAJA. NOR es el resultado de la negación del operador OR. También puede ser visto como una puerta AND con todas las entradas invertidas. El NOR es una operación completamente funcional. Las puertas NOR se pueden combinar para generar cualquier otra función lógica. En cambio, el operador OR es monótono, ya que solo se puede cambiar BAJA a ALTA, pero no viceversa.

En la mayoría, pero no en todas, las implementaciones de circuitos, la negación viene libre—incluyendo CMOS y TTL. En tales familias lógicas, el OR es la operación más complicada; puede utilizar un NOR seguido de un NOT. Una excepción importante es que algunas formas de la familia lógica dominó.

Simbolo:

                        

 Símbolo ANSI o "Militar"     Símbolo IEC       Símbolo DIN

INPUT		OUTPUT
A	B	A XOR B
0	0	0
0	1	1
1	0	1
1	1	0

La puerta XOR, compuerta XOR u OR exclusiva:

Es una puerta lógica digital que implementa el o exclusivo; es decir, una salida verdadera (1/HIGH) resulta si una, y solo una de las entradas a la puerta es verdadera. Si ambas entradas son falsas (0/LOW) o ambas son verdaderas, resulta en una salida falsa. La XOR representa la función de la desigualdad, es decir, la salida es verdadera si las entradas no son iguales, de otro modo el resultado es falso. Una manera de recordar XOR es "uno o el otro, pero no ambos".

La XOR también se puede ver como adición módulo 2. Como resultado, las puertas XOR se utilizan para implementar la adición binaria en las computadoras. Un semisumador consta de una puerta XOR y una puerta AND. También se utiliza como comparador y como inversor condicional.¹​

Las expresiones algebraicas ${\displaystyle A\cdot {\overline {B}}+{\overline {A}}\cdot B}$   ${\displaystyle \equiv }$   ${\displaystyle (A+B)\cdot }$ ( ${\displaystyle {\overline {A}}+{\overline {B}}}$ ) representan ambas la puerta XOR con entradas A y B. El comportamiento de la XOR se resume en la tabla de verdad mostrada a la derecha.

INPUT		OUTPUT
A	B	A XNOR B
0	0	1
0	1	0
1	0	0
1	1	1

La puerta XNOR u OR 

(a veces escrita "exnor" o "enor" y rara vez escrito NXOR) es una puerta lógica digital cuya función es la inversa de la puerta OR exclusiva (XOR). La versión de dos entradas implementa la igualdad lógica, comportándose de acuerdo a la tabla de verdad de la derecha. Una salida ALTA (1) resulta si ambas las entradas a la puerta son las mismas. Si una pero no ambas entradas son altas (1), resulta una salida BAJA (0).

Simbolo:

                                                

                             Símbolo XNOR "Distintivo"            Símbolo XNOR "Rectangular"

Evidecias del Laboratorio:

Circuito lógico:

Foto Grupal:

Link del vídeo :

                     https://www.youtube.com/watch?v=H-iSGNceVY8&feature=youtu.be

Observaciones: 

• En el programa proteus se debe buscar cada componente lógico mediante su código específico.
• Al momento de seleccionar los componentes lógicos en el programa proteus, se escogió erróneamente componentes similares a los necesarios para realizar el circuito.
• En la tabla de verdad existirá casos donde la salida puede ser “1”, pero por condiciones ambientales esos casos son imposibles que sucedan.
• En las pruebas de funcionamiento del circuito, el led final que representaba al toldo no encendía por un problema de conductividad en uno de los conectores empleados. 
• Se observo que las compuertas lógicas ayudan a combinar distintas funciones que permiten solucionar los problemas.
• Se observo que el programa virtual ayuda a encontrar las soluciones rápidamente sin necesidad de estar haciendo el mapa de Karnaugh.
• Es necesario hacer una tabla de verdad en una hoja para luego pasarla al programa que realiza el mapa de Karnaugh.

Conclusiones:

• Se realizó la tabla de verdad empleando las 4 variables y cumpliendo con cada una de las características que solicitaba el problema.
• Se logró obtener la ecuación simplificada y el mapa de Karnaugh mediante el software en línea www.32x8.com.
• Se utilizó correctamente el programa proteus para realizar y ejecutar las simulaciones del circuito electrónico.  
• En el desarrollo del laboratorio se identificó las puertas lógicas empleadas, su simbología y su comportamiento en la simulación del circuito electrónico con el programa proteus.
• Se demostró la importancia de obtener conocimientos de electrónica digital para emplearla en trabajos de automatización.
• El mapa de Karnaugh virtual ayudo a resolver las condiciones que nos pedía el laboratorio.
• Se cumplieron las funciones necesarias para resolver el circuito lógico que el laboratorio nos pedía.
• Se culmino todo el laboratorio correctamente sin problemas y se pudo utilizar las compuertas lógicas mediante un software.

LABORATORIO NRO. 1

PUERTAS Y FUNCIONES LOGICAS

FASE 1:

CONOCIENDO LAS FUNCIONES LÓGICAS, TABLAS DE VERDAD Y MAPA DE KARNAUGH

1. COMPETENCIA ESPECIFICA DE LA SESION:

• Comprobar las tablas de verdad de puertas lógicas y sus combinaciones. 
• Conocer las principales Puertas Lógicas, su simbología y comportamiento 
• Utilizar un SIMULADOR para comprobar el comportamiento de los mismos. 
• Utilizar métodos de simplificación de compuertas lógicas. 

2. MARCO TEÓRICO:

2.1 COMPUERTAS LÓGICAS: 

Una puerta lógica, o compuerta lógica, es un dispositivo electrónico con una función cuyo dominio son las palabras conformadas por los valores binarios 0 ó 1  u otras funciones como sumar o restar, incluyen o excluyen según sus propiedades lógicas.

        2.1.1 Compuerta SI o YES

       La puerta lógica SI realiza la función de igualdad. 

       La ecuación característica que describe el comportamiento de la puerta SI es:

        F=A

       Su tabla de verdad es la siguiente:

        2.1.2 Compuerta AND o Y

       Su símbolo es un punto (·), aunque se suele omitir. Así, el producto lógico de las variables A y B se

       indica como AB, y se lee A y B o simplemente A por B.

       Su tabla de verdad es la siguiente:

        

        2.1.3 Compuerta OR o O

      

         (${\displaystyle \scriptstyle OR\equiv O\equiv \lor }$), realiza la operación de suma lógica.

         La ecuasion característica que describe el comportamiento de la puerta OR es:

  F= A+B

         Su tabla de verdad es la siguiente:

        2.1.4 Compuerta NOT o NO 

        La puerta lógica NO o NOT realiza la función de inversión o negación de una variable lógica.

        Una variable lógica (A) a la cual se le aplica la negación se pronuncia como "no A" o "A negada"

  Su tabla de verdad es la siguiente:

 2.1.5 Compuerta NAND

        La puerta lógica NAND, realiza la operación de producto lógico negado.

        La ecuacion característica que describe el comportamiento de la puerta NAND es:

  Su tabla de verdad es la siguiente:

  2.1.6 Compuerta NOR

        La puerta lógica NOR realiza la operación de suma lógica negada. 

           La ecuación característica que describe el comportamiento de la puerta NOR es:

  Su tabla de verdad es la siguiente:

2.2 TABLAS DE VERDAD 

Una tabla de verdad,o tabla de valores de verdad, es una tabla que muestra el valor de verdad de una proporción compuesta, para cada combinación de verdad que se pueda asignar.

Una tabla de verdad ayuda a adquirir el funcionamiento deseado de un circuito integrado con compuertas lógicas asignado así a la tabla las variables de entrada A, B, C, etc. Obteniendo así el circuito idóneo que se desea obtener. 
Generalmente se utiliza una tabla con valores asignados de 0 y 1, donde 0 representa que el circuito esta negado o inactivo y 1 que el circuito esta operativo o activado.

2.3 MAPA DE KARNAUGH 

Es una herramienta muy utilizada para la simplificación de circuitos lógicos, cuando empleamos una función lógica con su tabla de verdad y se desea implementar esa función de la manera más reducida posible se utiliza este método.

El agrupamiento de ceros 0 y unos 1 dentro del mapa te ayuda a visualizar las relaciones lógicas entre las variables y conduce directamente a una función booleana simplificada. El mapa de Karnaugh es a menudo usado para simplificar los problemas lógicos con 2, 3 o 4 variables. Un mapa de Karnaugh de 2 variables es trivial pero puede ser usado para introducir el método que necesitas aprender.

2.3.1 Convertir la expresión a una suma de productos si es necesario. Esto se puede realizar de varias maneras:

• Algebraica mente.
• Construyendo una tabla de verdad, trasladando los valores al mapa de Karnaugh. Esta es la forma que vamos a utilizar.
  

2.3.2 Cubrir todos los unos del mapa mediante rectángulos de 2^N elementos, donde N = 0 ... número de variables. Ninguno de esos rectángulos debe contener ningún cero (tal y como indicábamos en el apartado anterior).

• Para minimizar el número de términos resultantes se hará el mínimo número posible de rectángulos que cubran todos los unos.
• Para minimizar el número de variables se hará cada rectángulo tan grande como sea posible.

2.3.3 Finalmente escribir la función lógica reducida, con los datos de la tabla anterior se procede a escribir un la función lógica reducida.

3. EVIDENCIA DE TAREAS EN LABORATORIO:

3.1 EVIDENCIA DE MATERIALES UTILIZADOS 

3.2 EVIDENCIA DE CIRCUITOS REALIZADOS 

3.3 VÍDEO

https://www.youtube.com/watch?v=x4BmE7pAcmA&t=281s

4. OBSERVACIONES:

• Para realizar la simulación del circuito en el programa PROTEUS se debe escoger el tipo de componente a usar mediante un código específico como AND, u OR.
• El primer componente lógico “&” que empleó el grupo de trabajo no funcionaba correctamente. 
• Los componentes lógicos empleados para armar el circuito tenían la característica de que sus leds se enciendan al insertarse al protoboard por un tema de construcción de fábrica. 
• Se observó que la compuerta lógica AND estaba averiada por lo cual se solicitó un cambio.
• Para realizar la simulación se tiene que abrir un Windows virtual ya que solo en este se puede abrir el programa de simulación.
• Se debe tener en cuenta todas las especificaciones del problema para poder realizar el diseño de los circuitos ya que este dependerá que tipo de compuerta lógica se va ha utilizar.
• No se presentaron inconvenientes ya que se pudo realizar a la perfección la prueba final del circuito. 

5. CONCLUSIONES

• Empleando tablas de verdad y el mapa de KARNAUGH se determinó que componentes lógicos se emplearan en el circuito.
• Se logró crear el circuito electrónico en el programa PROTEUS y ver su funcionamiento. 
• Se pudo Implementar circuitos de lógica combinacional y secuencial.
• Se comprobaron las tablas de verdad de puertas lógicas y sus combinaciones en un problema especifico.
• Se utilizó métodos de simplificación de compuertas lógicas como la tabla de KARNAUGH.

6. FOTO GRUPAL: